Excelで感染症流行を予測するSIRモデルを計算してみました！【簡単シミュレーション】

SIRモデルとは？

SIRモデル[1]は、人から人へ直接伝搬する感染症の流行を予測するための基本的な数理モデルです。

このモデルを用いることができる前提条件は以下となっています。

• 新型の感染症のため免疫を持つ人はいない。
• 外部の都市との間で人口移動がない。
• 人口は密集し不特定多数の人との接触がある。
• ペストのような急速かつ短期的な流行である。

SIRのそれぞれの文字は以下の英語の頭文字を取ったものです。

S: 感受性(Susceptible)
I: 感染性(Infectious)
R: 隔離や回復(Removed/Recovered)

つまり、注目する地域の人口を

感染する可能性のある人(S)、感染した人(I)、それ以外の人(R)に分けて

それぞれの時間的な変化をモデル化しています。

SIRモデルは時間変化の微分方程式なので、正式には以下で表記されます。[2]

今回はこれをExcelに落とし込むため、少し形式を変えて、以下のように表します。

SIRモデルを用いた簡単な感染症流行予測

この本を参考にしました。

※ちょっと数式が違っている…ので、気づいたら自分で直して使うといいと思います。

計算にあたって、まず必要な数値を決めていきます。

必要なのは以下です。

• 1日あたりの感染確率
• 1日あたりの回復確率
• 人口

上から順に決めていきましょう。

感染確率は5%［3］
濃厚接触の回数は3回（濃厚接触の定義は[4]参照）です。

したがって1日の感染確率は15%となります。
これをaとします。

a = 0.15

回復には平均2週間かかる[5]ので、1日の回復率は7%です。
回復率をbとします。

b = 0.07

あとは適当な初期値（人口と感染者数）を与えれば、計算することができます。

今回は身近な例として、東京都を想定して計算してみます。

東京都の人口は約1000万人です。

最初の感染者は1人としましょう。

Excelに落とし込むと以下のようになります。

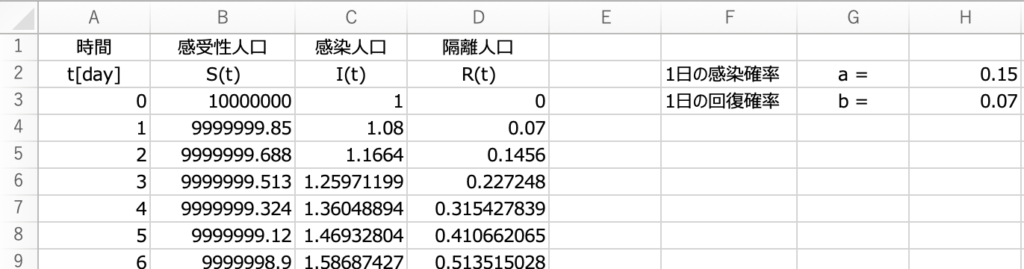
A列　時間（単位は[日]）
B列　感染の可能性のある人数（感受性人口）
C列　感染者数（感染人口）
D列　それ以外（回復した人数、隔離人口）
H列2行目　1日の感染確率
H列3行目　1日の回復確率

B3, C3, D3セルにはそれぞれの初期値が入力してあります。

B4セルには以下の式が入ります。

B4 = B3 – $H$2 * B3 * C3 / $B$3

前日の感受性人口から、感染人口を引いたモノです。

C4セルには以下の式が入ります。

C4 = C3 + $H$2 * B3 * C3 / $B$3 – $H$3 * C3

前日の感染人口に、新しく感染者を加え、そこから回復者の数を引いたモノです。

D4セルには以下の式が入ります。

D4 = D3 + $H$3 * C3

前日の隔離人口に、新しい隔離人口を足したモノです。

結果のグラフを次のセクションに示します。

結果

Excelでの計算結果を以下に示します。

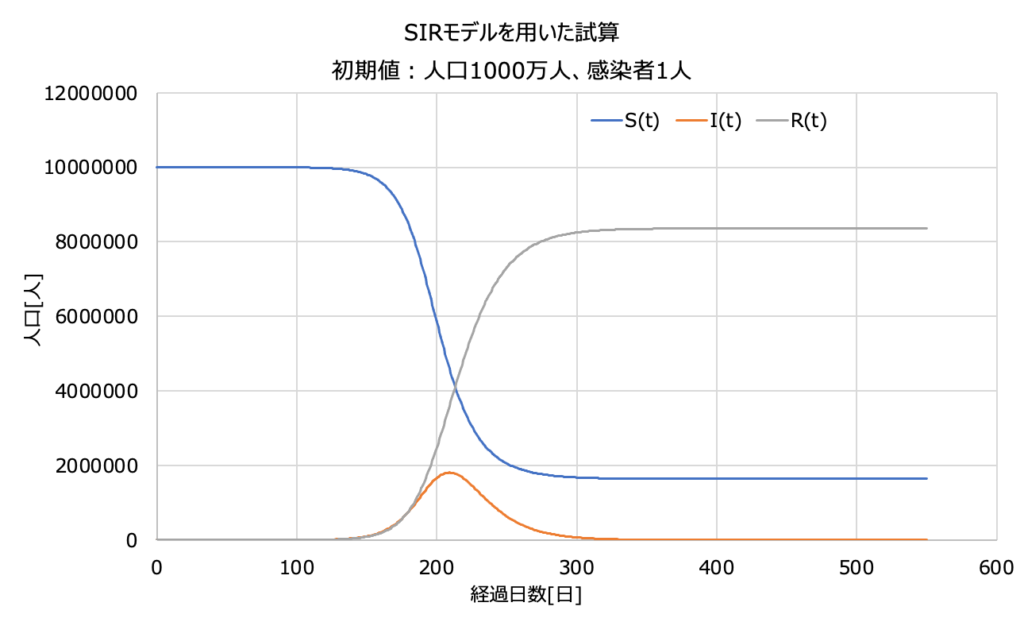
最初の100日間程度は何も起こらないですね。

100日後は徐々に感染者数（オレンジ線）が増えていき、

最大で約180万人に到達します。

これが最初の感染から約7ヶ月後です。

感染者数が増えたということは、未感染の人口が減ったということですので、

その後は感染者数は減少していきます。

そして、ピークから約3ヶ月後には終息します。

東京都民のうち約８割が感染してやっと終了ということです。

なかなか絶望的・・・

それにしても、180万人はものすごい数ですね。

東京都の病院ベッド数が約10万床[6]なので、圧倒的に医療崩壊です。

そこで次に、1日の感染確率を減らして計算してみることにします。

例えばマスクをすると、感染確率は下がります。

新型コロナを発症した人が症状が出る前からマスクを着けていた場合、家族への感染が79％減ったという報告[7]があるので、

これを参考にします。

家族＝濃厚接触者と考えて、感染確率を15%から79%減らして

0.15×(1-0.79)=0.03

ただ、マスクが義務化されるのは少なからず感染が拡大してきた頃だと思うので、

感染者が約1万人となった、120日目以降の感染確率を、3%としてみます。

この場合の計算結果は以下になります。

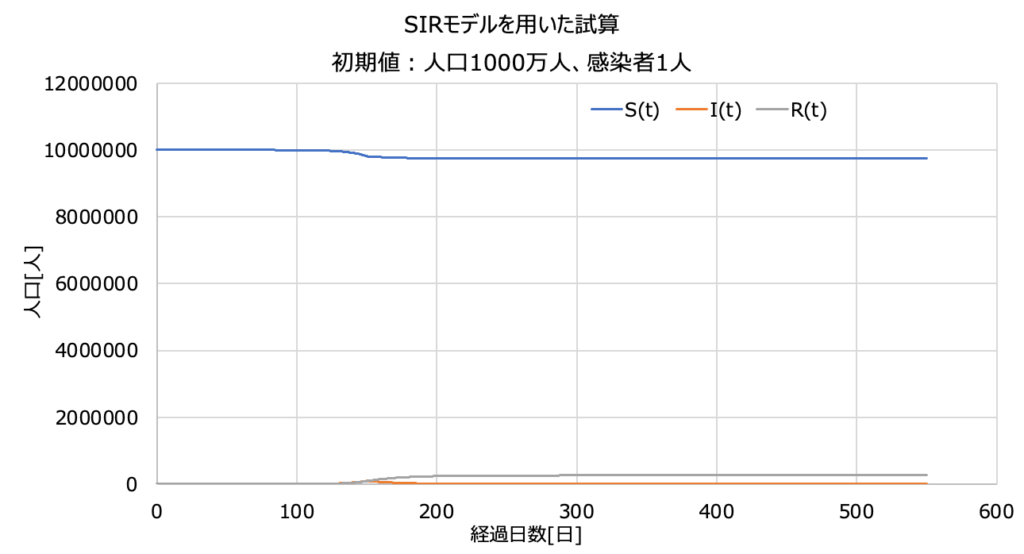
感染確率15％の時とは、だいぶ違いますね。

感染者数が約1万人に到達した120日目以降、全員が徹底してマスクをつければ、

120日目がピークとなり、以降は減少に転じます。

上の図では縦軸が大きすぎて減少の様子が見えないので、拡大します。

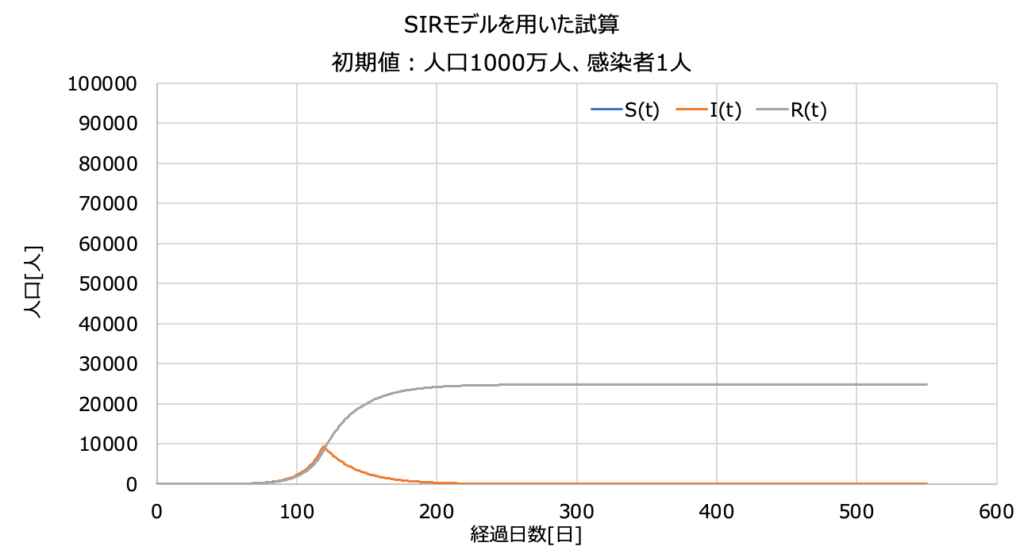
ピークとなる120日目から、約90日（3ヶ月）ほどで終息しています。

東京都民のうち約0.3割（２万５千人）が感染して終了となります。

ちょっと極端に感染確率を減らしすぎたかもしれません。。

みなさんも自分のExcelで計算してみてください。

考察

実際の東京都の感染者状況は、2021年4月16日現在以下のようになっています。[7]

地域	感染者数	回復者数	死亡者数
東京都	12.8万	12.1万	1,812

日ごとの陽性者数は以下のように推移しています。[8]

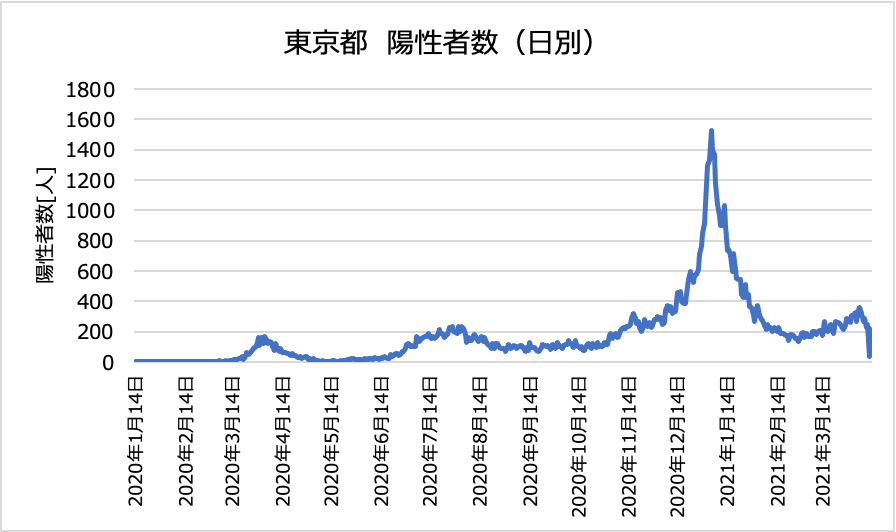
このグラフと図３を比較して見ると、以下のことが考えられます。

• 2020年4月中旬に何らかの感染対策が行われ、感染確率が減少。
• 2020年6月下旬ごろから感染対策が失速し、再び感染確率が増加。
• 2020年9月〜11月の間は増加も減少もしていない（＝感染確率と回復率が釣り合っている）
• 2020年12月以降、感染確率が急増。
• 2020年12月末に何らかの感染対策が行われ、感染確率が減少。
• 無事収まったかに見えたが、2021年2月末以降再び緩やかな増加？

何らかの感染対策というのは緊急事態宣言でしょうか？

個人的には、
・緊急事態宣言後の3ヶ月ほど、感染者数が横ばいになっている
・12月末に急に増えた
ことが少し不思議です。

12月はイベント多いので、そこで感染が広がったのかもしれません。

素人の分析ですが、自分の手で計算ができると、

色々想像できて面白いです。

簡単な計算ではありますが、行政のデータ開示があるため答え合わせができる　＆　万全の感染対策をしようと思える内容なので、コロナウイルスの感染シミュレーションは結構興味深いかなと思います。

他のテーマでも簡単にシミュレーションしてみたいと思います。

参考文献

1. W. O. Kermack and A. G. McKendrick, “A Contribution to the Mathematical Theory of Epidemics,”Proc. Roy. Soc. of London. Series A, Vol. 115, No. 772 (Aug. 1, 1927)(https://doi.org/10.1098/rspa.1927.0118)
2. 感染症の数理モデルと対策 – 日本内科学会 (https://www.naika.or.jp/jsim_wp/wp-content/uploads/2020/11/nichinaishi-109-11-article_4.pdf)
3. Klompas M, et al. Airborne transmission of SARS-CoV-2: Theoretical considerations and available evidence. JAMA. 2020;324(5):441-442. (https://jamanetwork.com/journals/jama/fullarticle/2768396)
4. 新型コロナウイルス感染症患者に対する積極的疫学調査実施要領(https://www.niid.go.jp/niid/images/epi/corona/COVID19-02-210108.pdf)
5. Report of the WHO-China Joint Mission on Coronavirus Disease 2019 (COVID-19)(https://www.who.int/docs/default-source/coronaviruse/who-china-joint-mission-on-covid-19-final-report.pdf)
6. JMAP地域医療情報システム　都道府県別統計　東京都 (http://jmap.jp/cities/detail/pref/13)
7. JHU CSSE COVID-19 Data
8. 東京都 (https://stopcovid19.metro.tokyo.lg.jp/cards/positive-number-by-developed-date/)

以下の本、以前も紹介しましたがおすすめです。

関連記事はこちら

【Excelで科学技術計算】おすすめの本4冊【エンジニア向け】