ポアソン分布の導出【統計検定2級】

統計検定2級を受検する方や、統計になんとなく興味がある方は聞いたことがあるであろう「ポアソン分布」

かの有名な統計WEBにも、ポアソン分布の式は二項分布から導出すると書いてあります。

しかし式の導出は統計WEBには載っていなかったため、記事にしてみました。

　

　

ポアソン分布とは何か

ポアソン分布とは、ある一定区間の中で、偶然に起こる事象の数の分布です。

「偶然に起こる事象」というのがポイントです。

偶然に起こる事象というのは、例えば交通事故が良い例でしょう。

発生件数が多い場合はポアソン分布の式では再現できなくなり、正規分布に近くなります。

ポアソン分布の導出

では早速ポアソン分布を導出します。

試行回数　n回
事象発生回数　X回
事象発生確率　p
期待値　λ (λ＝n×p)

ここで、X＝k(k回事象が起きる)となる確率を求めることとします。

この時の二項分布の式、及び、そこから導かれるポアソン分布の式はこちら

　

ポアソン分布は試行回数nが十分大きく、確率pが小さいという定義なので、nを∞、pを0に近づけています。

ポアソン分布の式の完成形を把握したところで、順に式を導出していきましょう。

　

まずは二項分布の式を変形

　

このnCkは以下のように変形します。

1行目はnCkの定義通りで、2行目は全ての項をnで割っています。

理由はn→∞を使いたいからです。

　

　

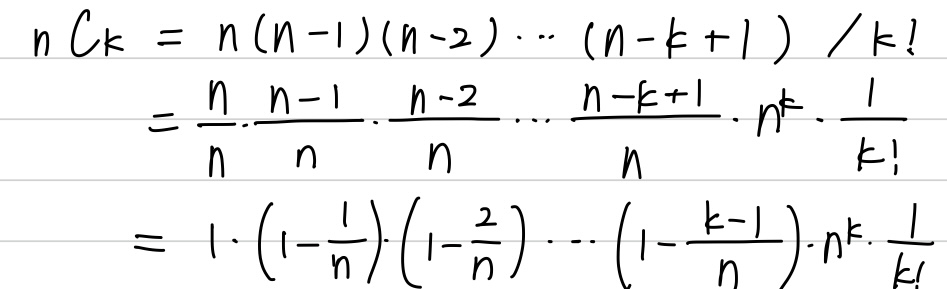
こうするとn→∞で1/n→0にできますね。

これを元の式に代入します。

元の式はこれ

　　

ここにnCkを代入すると

　

　

1/k!はこれ以上どうしようも無いので放置します。

(np)^kは期待値λ＝npを使ってλ^kと変形できます。

最後に残ったのが、最後の項、(1-p)^(n-k)ですね。

これをどうにかしていきます。

まず1-pのpをなんとかしたいので、期待値λ=npを使ってp=λ/nとします。

そうするとn→∞が使えそうです。

　

勘の良い方または高校生の方は気づくかも知れませんが、ネイピア数の定義を使います。

(社会人は大半の方が忘れていると思いますw（私もすっかり忘れていた））

　

　

ネイピア数の定義のxの部分がーλとなります。

　

以上より、ポアソン分布の式が導けます。

　

(字が汚くてすみません)

　

終わり

式の導出って意外と載っていないんですよね。

高校数学を思い出したい26歳社会人です。